Step 2 Yes, it is a 345 triangle for n = 2 Step 3 Calculate the third side 5n = 5 × 2 = 10 Answer The length of the hypotenuse is 10 inches Example 2 Find the length of one side of a right triangle if the length of the hypotenuse is 15 inches and the length of the other side is 12 inches Solution3^211^2=c^2 c=√130 Step 4 Plug in a, b, and c for o, a, and h respectively in each corresponding ratio sinθ=3/√130 cscθ=√130/3Ex Find the exact values of all 6 trigonometric functions of the angle θ shown in the figure SOLUTION first you'll need to determine the 3rd side using ab22 =c2 Æ a22=5132 Æ a =12 So for the angle labeled θ, ADJACENT = 12, OPPOSITE = 5 and HYPOTENUSE = 13 opp 5 sin hyp 13 θ== adj 12 cos hyp 13 θ== opp 5 tan adj 12 θ== hyp 13 csc opp 5 θ==

Pythagorus Theorum Math Lesson 3 4 5 Triangle Youtube
6 trig functions of 3 4 5 triangle
6 trig functions of 3 4 5 triangle-Section 43 Right Triangle Trigonometry 301 The Six Trigonometric Functions Our second look at the trigonometric functions is from a right triangle perspective Consider a right triangle, with one acute angle labeled as shown in Figure 426 Relative to the angle the three sides of the triangle are the hypotenuse, theInverse trig functions arcsine, arccosine, and arctangent Now let's look at the problem of finding angles if you know the sides Again, you use the trig functions, but in reverse Here's an example Suppose a = 123 and b = 501 Then tan A = a/b = 123/501 = Back when people used tables of trig functions, they would just look up
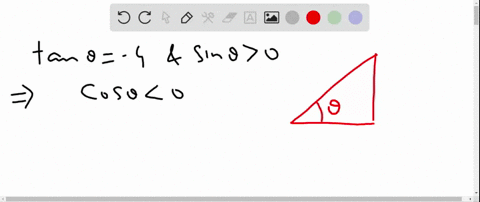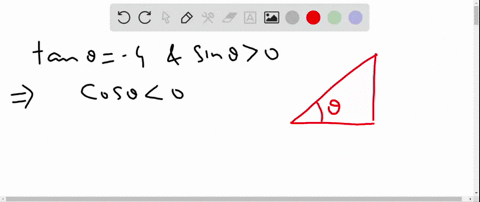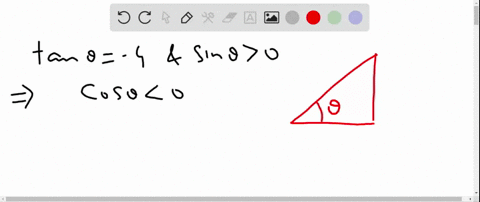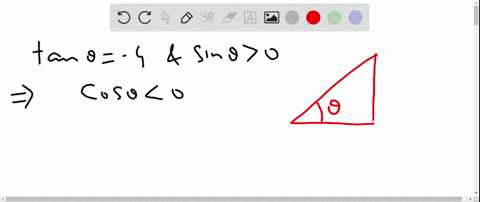



Solved Find The Values Of The Trigonometric Functions Of Theta From The Information Given Tan Theta Frac 3 4 Quad Cos Theta 0
Step 3Find the missing side by using the Pythagorean Theorem a^2b^2=c^2 *remember a=altitude (opposite side) b=base (adjacent side) c=hypotenuse a=3 b=11 c=?First way You can familiarize yourself with the unit circle we talked about An ordered pair along the unit circle (x, y) can also be known as (cos 𝜃, sin 𝜃),Day 3 Using Trigonometry to Determine Area SWBAT Derive the formula for calculating the Area of a Triangle when the height is not known Day 4 Law of Sines SWBAT Find the missing side lengths of an acute triangle given one side length and
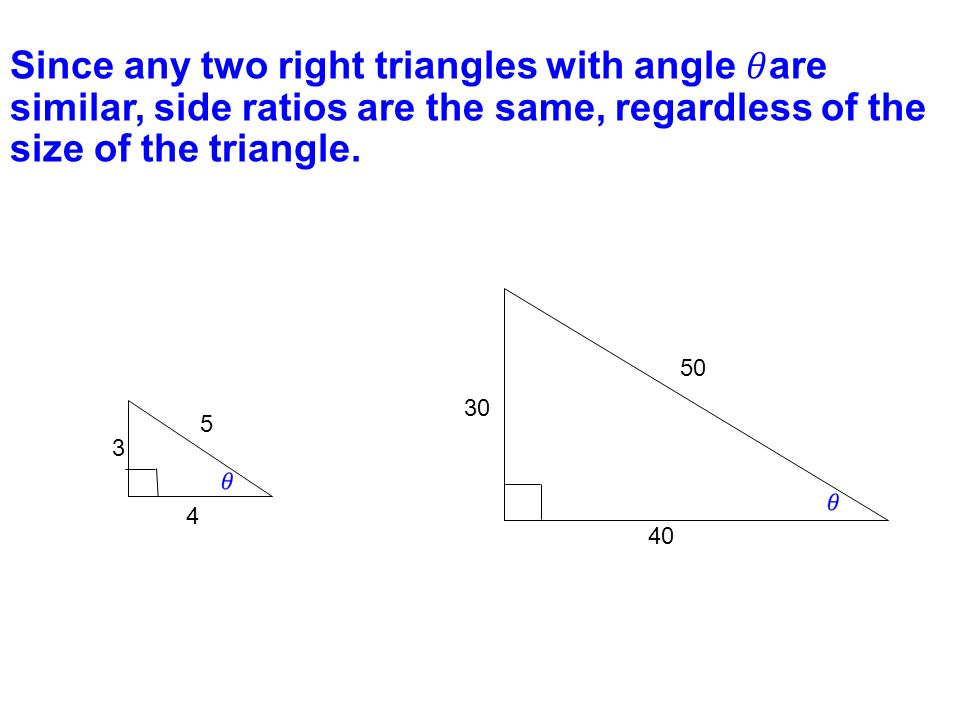
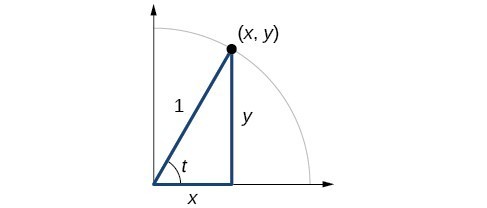
A a a is the length of the "adjacent" side, b b b is the length of the "opposite" side, and c c c is the length of the hypotenuse Then the basic trigonometric functions can be expressed as follows sin θ = opposite hypotenuse, cos θ = adjacent hypotenuse, tan θ = opposite adjacentNotes 43 Right Triangle Trig Hand outs Right Triangle Trig4 3 4 = opposite side of 2 3 8 4 3 cos hyp adj D 3 2 secD 2 1 8 4 sin hyp opp D cscD 2 3 1 4 3 4 tan adj opp D cotD 3 NOTE These answers should look familiar to you The angle would have to be the 30q or 6 S angle Examples Use a right triangle to find the exact value of the other five trigonometric functions if given the following 1 7 3 sin E
Answer (1 of 4) x = 4 ;Precalculus (6th Edition) Blitzer answers to Chapter 4 Section 43 Right Triangle Trigonometry Exercise Set Page 561 21 including work step by step written by community members like you Textbook Authors Blitzer, Robert F, ISBN10 , ISBN13 , Publisher Pearson45 3 Figure 431 A particular acute angle always gives the same ratio of opposite to adjacent sides In general,the trigonometric function values of depend only on the size of angle and not on the size of the triangle Evaluating Trigonometric Functions Find the value of each of the six trigonometric functions of in Figure 432
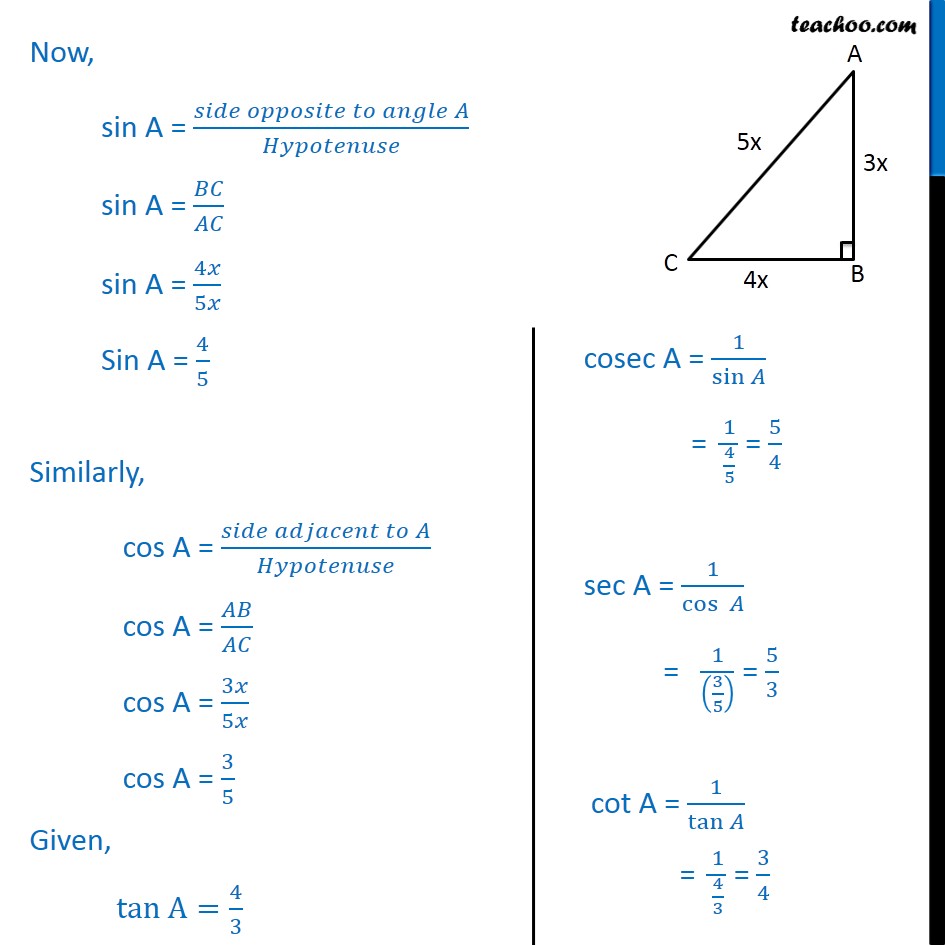



Example 1 Given Tan A 4 3 Find Other Ratios Chapter 8 Class 10




3 4 5 Triangle Definition Math Open Reference
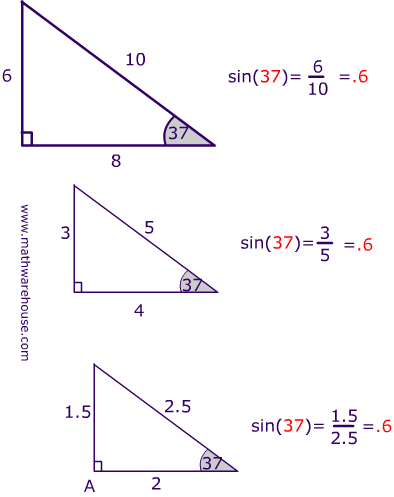
Section_43__angle_of_elevationdepressionpdf File Size 175 kb File Type pdf Find the trig functions given a 3, 4, 5 triangleSome worked problems using similar triangles 1 Find sec( ) if sin( ) = 3 5 Solution Draw a right triangle which has an angle with sin( ) = 3 5 (A 345 triangle will do) Then compute the secant of the angle The secant is the reciprocal of cosine and so sec( ) = hyp adj = H A The answer is 5 4 Smith (SHSU) Elementary Functions 13 7



Section 4 3 Right Triangle Trigonometry Precalculus




Right Triangles
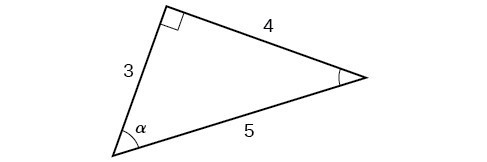
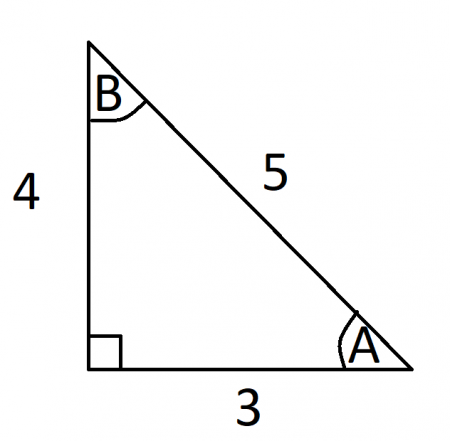
Section 54 The Other Trigonometric Functions In the previous section, we defined the sine and cosine functions as ratios of the sides of a right triangle in a circle Since the triangle has 3 sides there are 6 possible combinations of ratios While the sine and cosine are the two prominent ratios that can be formed, there are four others, andIn a 345 triangle = ABBCCA we know CA = 5 is the hypotenuse and its opposite angle B is 90 degrees Sin(90 degrees) = 1 so in the sin rule we have 5/1 = 4/sin(A) = 3/sin then Sin(A)=4/5 and sin=3/5 We also know A C = 90 so sin=3 /5 = 06 means (with an inverse sin calculator) that C= and then A=4 LawofSines c a b Figure 34 Sample triangle Example 5 is suggestive of a general rule called the LawofSines Specifically,given the sample triangle in Figure 34 with sides a,b, and c opposite the angles α,β, and γ respectively,the Law of Sines states that



Warm Up 3 24 25 What Are Three Basic Trigonometric Functions And The Their Ratios Sine Sin Cosine Cos Tangent Tan Ppt Download




Pythagorus Theorum Math Lesson 3 4 5 Triangle Youtube
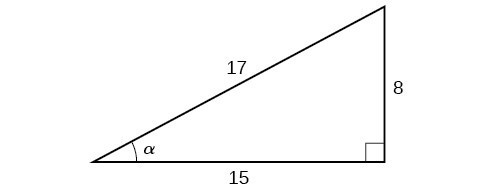
Figure 1431 3 A right triangle with side lengths of 8, 15, and 17 Angle alpha also labeled which is opposite to the side labeled 8 Solution The side adjacent to the angle is 15, and the hypotenuse of the triangle is 17, so via Equation cos ( α) = adjacent hypotenuse = 15 17 Exercise 1431 1For any right triangle, there are six trig ratios Sine (sin), cosine (cos), tangent (tan), cosecant (csc), secant (sec), and cotangent (cot) Here are the formulas for these six trig ratios Given a triangle, you should be able to identify all 6 ratios for all the angles (except the right angle)Everything in trigonometry seems to revolve around the 90 degree triangle and its ratios A 90 degree triangle is defined as a triangle with a right angle or in other words a ninety degree angle Given any known side length of a 90 degree triangle and one other value (another side, angle, area value, etc), one can find all unknown values of the



3




How To Find The Exact Value Of The Five Remaining Trigonometric Functions Youtube
Y = 3 ;= 3(2) 4(2) ?Reviewed by Hansun To, Professor of Mathematics, Worcester State University on 6/25/, updated 7/21/ Comprehensiveness rating 3 see less This textbook is a fourchapter comprehensive collection of Trigonometry topics including right triangle, graphing, identities of Trigonometric functions and Law of sines and cosines



Pictures Of 3 4 5 Right Triangles Free Images That You Can Download And Use




Multiple Representations For Trigonometric Equations Continuous Everywhere But Differentiable Nowhere
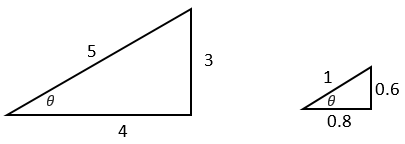
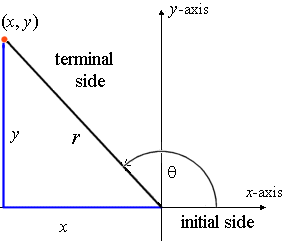
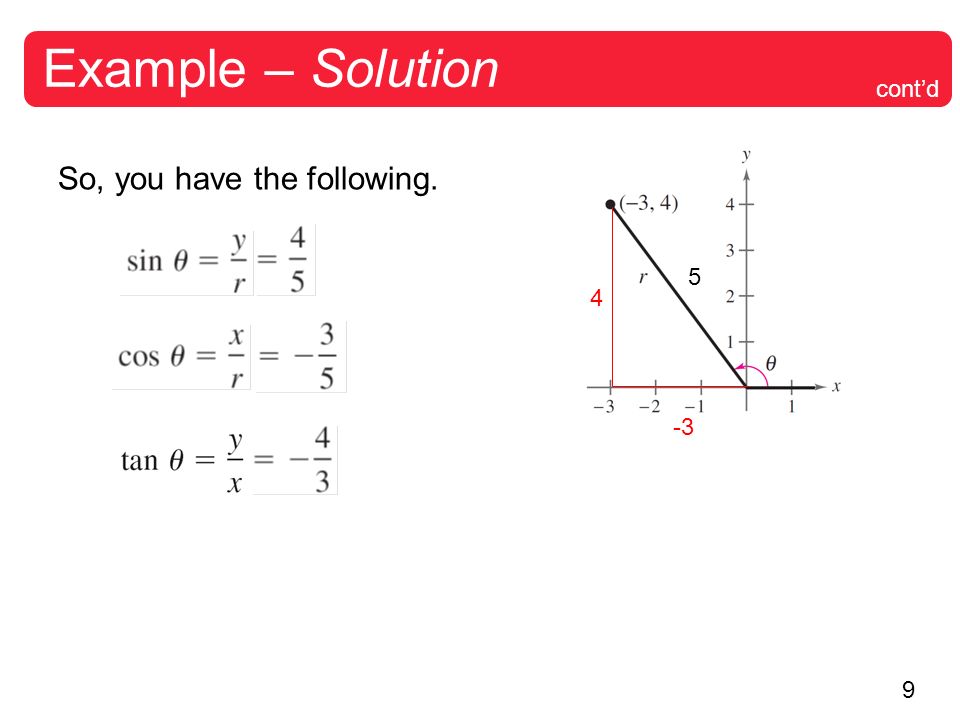
R = sqrt( x² y²) = 5 sin = y/r = 3/5 cos = x / r = 4/5 tan = x/y =4/3 = 4/3 cosec = r/y =5/3 = 5/3 sec = r/x =5/4 =5/4Precal Matters Notes 53 Circular Trig Functions Page 1 of 6 Chapter 53 Circular Trigonometric Functions Definition A reference triangle is formed by "dropping" a perpendicular (altitude) from the terminal ray of a standard position angle to the xaxis, that is, again, the xaxis The reference angle will be the positive, acute angleFind the value of trig functions given an angle measure Suppose you know the value of 𝜃 is 45°, how can this help you find the values of the six trigonometric functions?



Math Scene Trigonometry Sine Cosine And Tangent Lesson 1




Ppt Trigonometric Ratios Triangles In Quadrant I Powerpoint Presentation Id
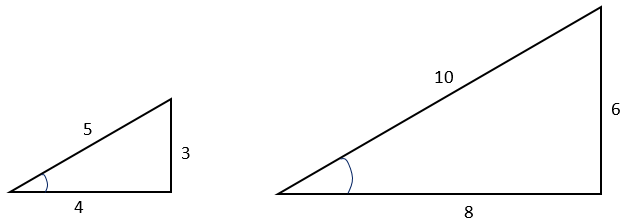
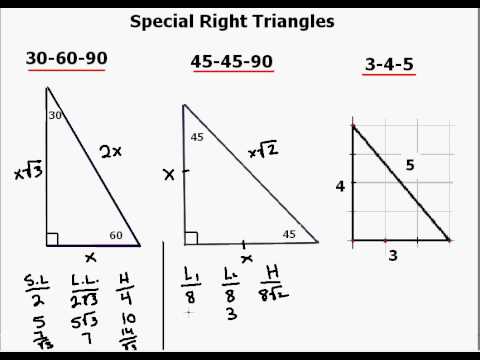
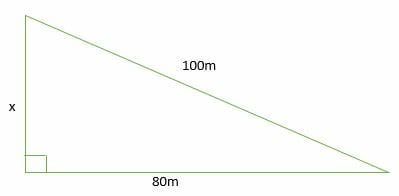
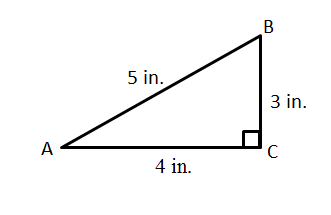
Trigonometry * Instant Trig Trigonometry is math, so many people find it scary It's usually taught in a onesemester highschool course However, 95% of all the "trig" you'll ever need to know can be covered in 15 minutes And that's what we're going to do now Angles add to 180° The angles of a triangle always add up to 180° 44° 68° 68° ° 1° 30° 44° 68° 68° 180°Example 2 A right triangle has side lengths 3 3 cm and 4 4 cm Find the length of the hypotenuse Substitute a= 3 a = 3 and b = 4 b = 4 into the Pythagorean Theorem and solve for c c a2b2 =c2 3242 =c2 916 =c2 25 =c2 c2 =25 √c2 =√25 c =5 cm a 2 b 2 = c 2 3 2 4 2 = c 2 9 16 = c 2 25 = c 2 c 2 = 25 c 2 = 25 c = 5 c mThe 345 triangle is useful when you want to determine if an angle is a right angle For example, suppose you have a piece of carpet and wish to determine if one corner of it is 90° First measure along one edge 3 feet The measure along the adjacent edge 4 ft




3 4 5 Triangle Angles Sides How To Solve Full Lesson




Ch 4 Trigonometric Functions Ppt Download
Chapter 5 Trigonometric Functions of Angles In the previous chapters we have explored a variety of functions which could be combined to form a variety of shapes In this discussion, one common shape has been width of the triangle to be 5 and the vertical height to be 3 From these we can find the distance between the points using the In fact, we can evaluate the six trigonometric functions of either of the two acute angles in the triangle in Figure \(\PageIndex{5}\) The side opposite one acute angle is the side adjacent to the other acute angle, and vice versa Unfortunately, the answer isn't given in x x 's as it should be So, we need to write our answer in terms of x x We can do this with some right triangle trig From our original substitution we have, sec θ = 5 x 2 = hypotenuse adjacent sec θ = 5 x 2 = hypotenuse adjacent This gives the following right triangle




Calculating Angles For A 5 12 13 Triangle Video Lesson Transcript Study Com




Right Triangles
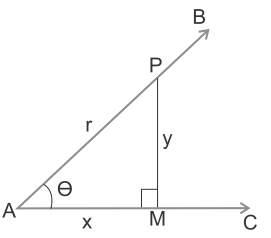
35 Trigonometric Functions Reference Evans 61 Consider a rightangled triangle with angle θ and side lengths x, y and h as shown θ x y h The trigonometric functions sine, cosine and tangent of θ are defined as sin θ = opposite hypotenuse = y h, cos θ = adjacent hypotenuse = x h tan θ = opposite adjacent = y x = sin θ cos θ 713 p 5) Now read o the values of the various trig functions cos = 2 7;sin = 3 p 5 7;tan = 3 p 5 2 The reciprocals of these are sec = 7 2;csc = 7 3 p 5 = 2 p 5 15;cot = 3 p 5 = 2 p 5 15 442 Applications with right triangles514 Apply trig functions and inverse trig functions to real world situations GSRT8 Angles of Elevation and Depression Apply trigonometry and the Pythagorean Theorem in context 521 Apply short cut ratios of special right triangles ( and ) to find missing side lengths GCO10 GSRT8 Special Right Triangles Part 1



Using Trigonometry Nz Maths



Section 4 3 Right Triangle Trigonometry Precalculus
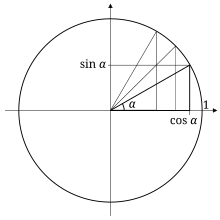
Trigonometry 5354 Trig Functions of Any Angle 1 Homework grades this week 01 Read sections 53 and 54 in your textbook (and 52 if you haven't already) by Monday 22 Aug 02 Complete at least 45 minutes of exercises on Khan Academy related to sections 52, 53, and 54 byFind Trig Functions Using Triangle Sides csc (x)=5/3 , tan (x)=3/4 Identify the known sides of the triangle using csc(x) = 5 3 csc ( x) = 5 3 Identify the known sides of the triangle using tan(x) = 3 4 tan ( x) = 3 4 Use hyp = 5 hyp = 5 and opp = 3 opp = 3 to find the value of the sine function Use hyp = 5 hyp = 5 and adj = 4 adj = 4 toPlot of the six trigonometric functions, the unit circle, and a line for the angle = radians The points labelled 1, Sec(θ), Csc(θ) represent the length of the line segment from the origin to that point Sin(θ), Tan(θ), and 1 are the heights to the line starting from the axis, while Cos(θ), 1, and Cot(θ) are lengths along the axis starting from the origin



Special Right Triangle Explanation Youtube




4 2 Trigonometric Functions Of Acute Angles Manualzz
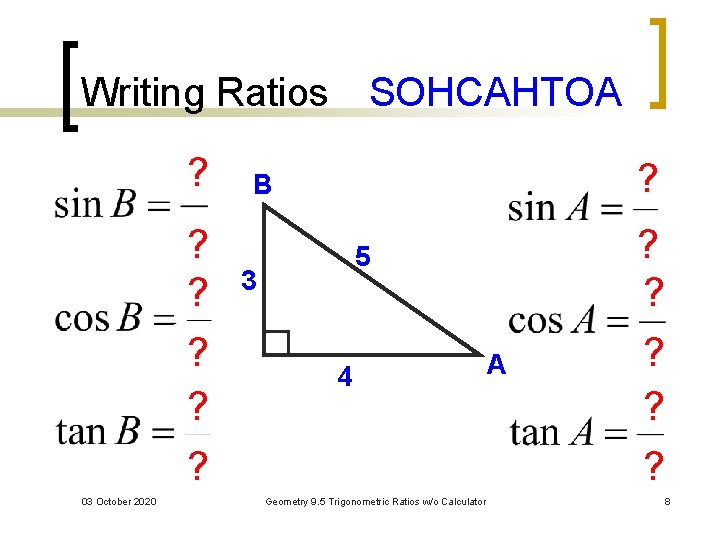
Solving for a side in a right triangle using the trigonometric ratios Sort by Top Voted Trigonometric ratios in right triangles Trigonometric ratios in right triangles Up Next Trigonometric ratios in right triangles Our mission is to provide a free, worldclass education to anyone, anywhere9 5 = 3 p 5 So y= 3 p 5 and our line segment ends at the point P(2;43 Right Triangle Trigonometry The second way that the six trig functions can be defined is through a right triangle Right Triangle Definitions of Trigonometric Functions Let θ be an acute angle of a right triangle The six trigonometric functions of the angle θ are defined as follows sin cos tan csc sec cot opp adj opp hyp hyp adj hyp




Trig Ratios Of Special Triangles Article Khan Academy



Math Scene Trigonometry Sine Cosine And Tangent Lesson 1
This video explains how to determine all six trigonometric function values using a reference triangle for 5pi/4 radiansmathispower4ucomStep 1 Test the ratio of the lengths to see if it fits the 3n 4n 5n ratio 6 8 ?Section 43 Exercises 1 The 450° angle lies on the positive–y axis (450°360°=90°), while the others are all coterminal in Quadrant II 2 The angle lies in Quadrant I , while the others are all coterminal in Quadrant IV In #3–12, recall that the distance from the origin is r= 3 sin ¨= , cos ¨=– , tan ¨=–2;



9 5 Trigonometric Ratios Sine And Cosine Geometry




1 18 Videos Some Practice Problems 1 Using The Chegg Com
Definition of the Trig Functions Right triangle definition For this definition we assume that 0 2 p2 Label the given sides of the triangle Since trigonometric expressions represent ratios of the sides of right triangles, two sides are always given 3 Determine algebraically the 3rd side 4 Write the expression asked for (outside expression) EXAMPLES Rewrite each trigonometric expression as an algebraic expression involving the variable u




Lesson Explainer Solving Trigonometric Equations With The Double Angle Identity Nagwa




Trigonometry
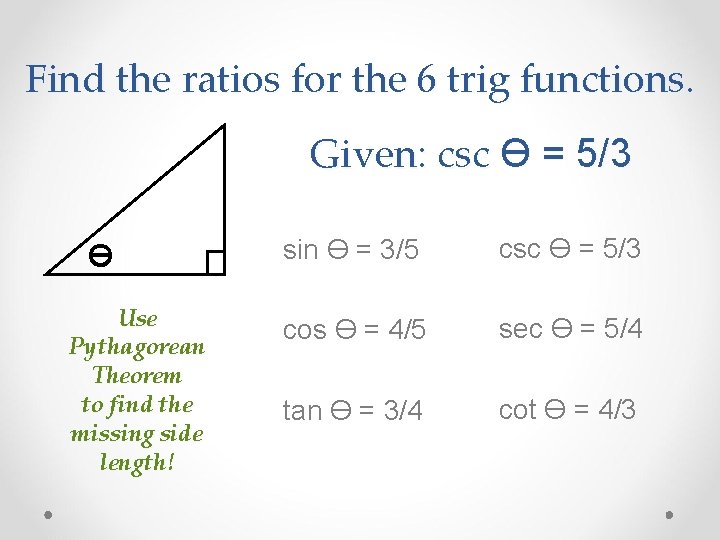



Trigonometric Ratios Triangles In Quadrant I A Trig




Trigonometry Ratios In Right Triangle




5 12 13 Triangle Angles Sides How To Solve Full Lesson



3 4 5 Right Triangles Explanation Examples



Introducing Trigonometry



Special Right Triangle Wikipedia




Trigonometry Wikipedia



Right Triangle Trigonometry Precalculus Ii




Find The Tangent Of Angle Y A 3 4 B 3 5 C 4 5 D 5 4 Study Com



What Is Cos 0 Equal To Science Trends




Question 1 Triangle Abc Has Side Lengths Of Ab3 5 Chegg Com



Quadrant




The 3 4 5 Triangle Ssdd Problems




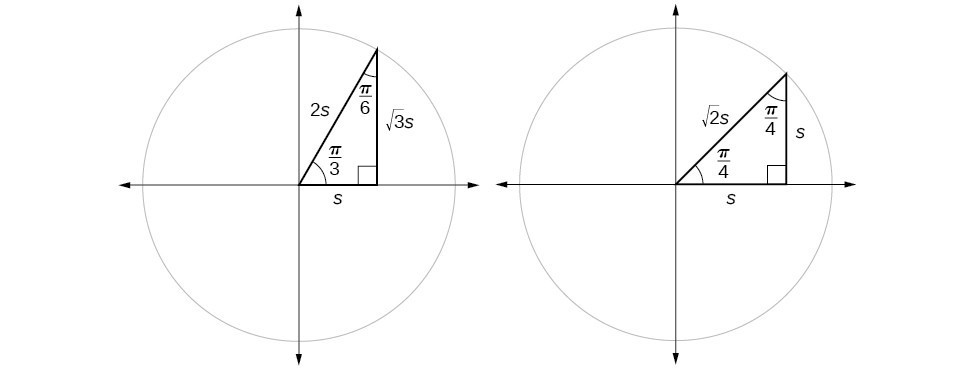
Lesson Explainer Evaluating Trigonometric Function Values With Angles 30 45 And 60 Nagwa




4 2 Trigonometric Functions Of Acute Angles Manualzz
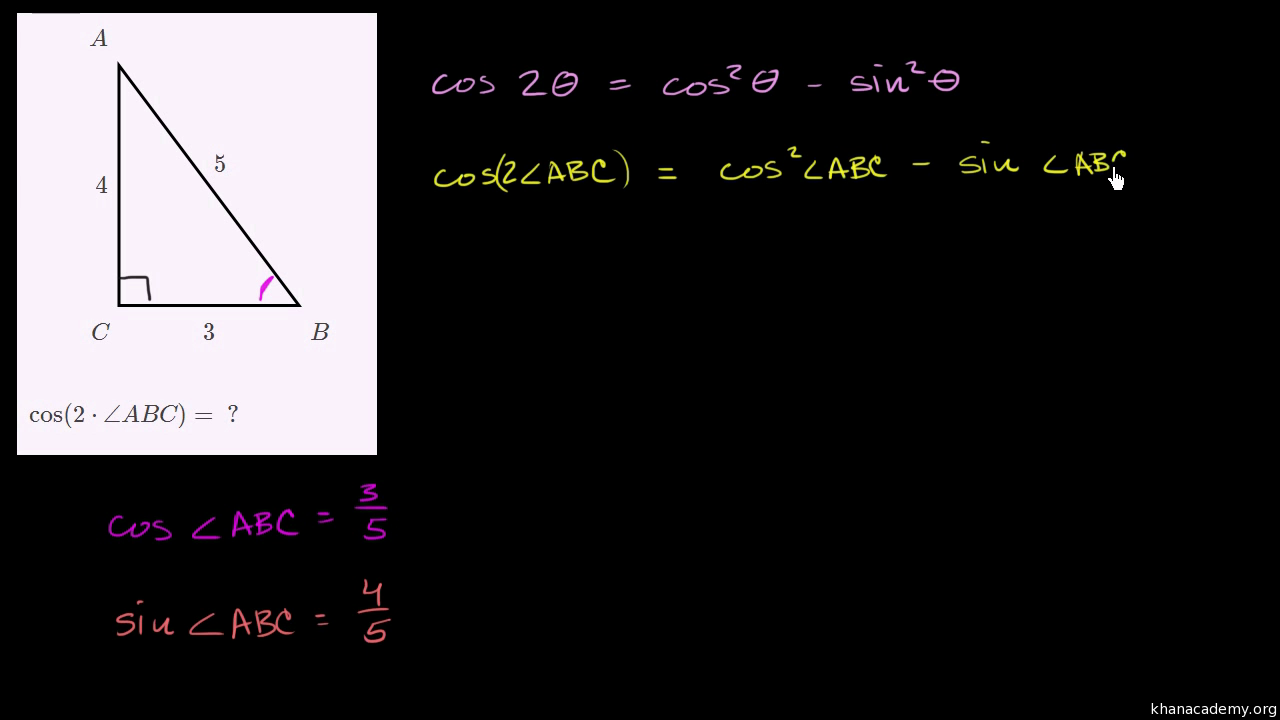



Module 4 Trigonometry Precalculus Eureka Math Engageny Khan Academy




Unit 8 Trigonometric Functions Radian And Degree Measure Unit Circle Right Triangles Trigonometric Functions Graphs Of Sine And Cosine Graphs Of Other Ppt Download



The 6 Trig Ratios




Trigonometry
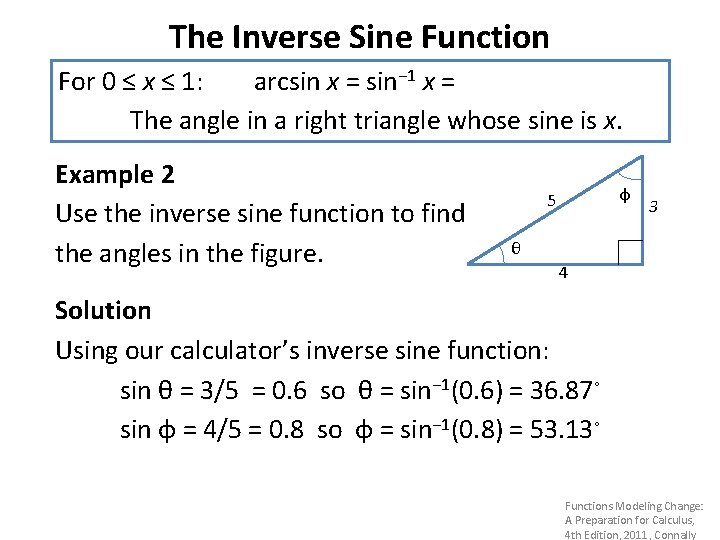



7 5 Right Triangles Inverse Trigonometric Functions Functions




Trigonometric Functions Justin Skycak



1




Solved Find The Values Of The Trigonometric Functions Of Theta From The Information Given Tan Theta Frac 3 4 Quad Cos Theta 0



Section 4 3 Right Triangle Trigonometry Precalculus



Basic Trigonometric Functions Trigonometry Socratic



Quadrant
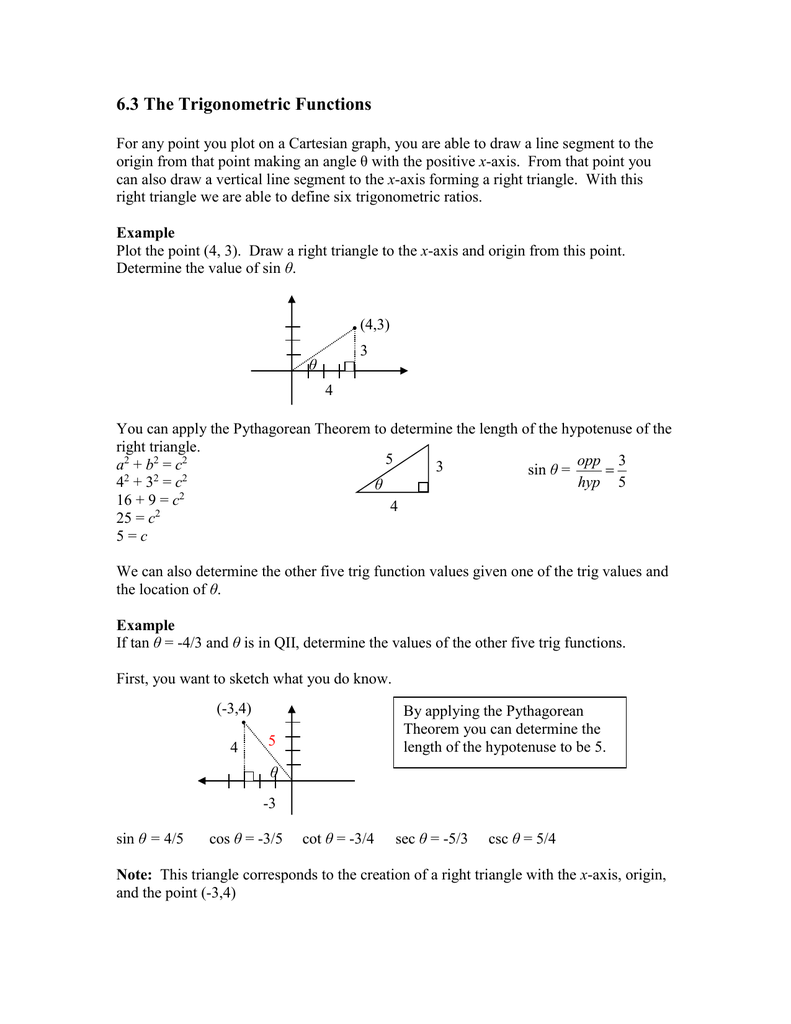



6 3 The Trigonometric Functions



Trigonometric Ratios Table Formulas Definitions Mnemonics Problems




Example 1 Given Tan A 4 3 Find Other Ratios Chapter 8 Class 10



Math Scene Trigonometry Sine Cosine And Tangent Lesson 1



5 Signs Of The Trigonometric Functions



Math Scene Trigonometry Sine Cosine And Tangent Lesson 1




Special Right Triangles 3 4 5 Triangle Study Com



Right Angle Trigonometry



Trigonometric Functions Of Any Angle Evaluate Trigonometric Functions Of Any Angle Find Reference Angles Evaluate Trigonometric Functions Ppt Download



3 4 5 Right Triangles Explanation Examples
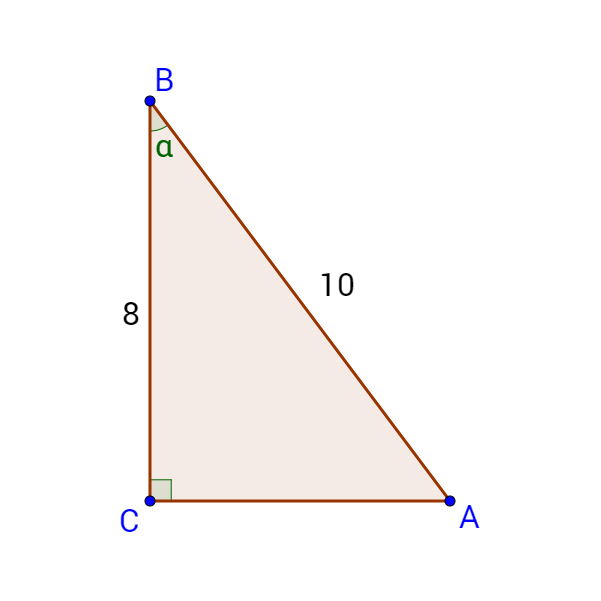



4 03 Right Triangle Trigonometry



Cosecant Cosecant Function Csc
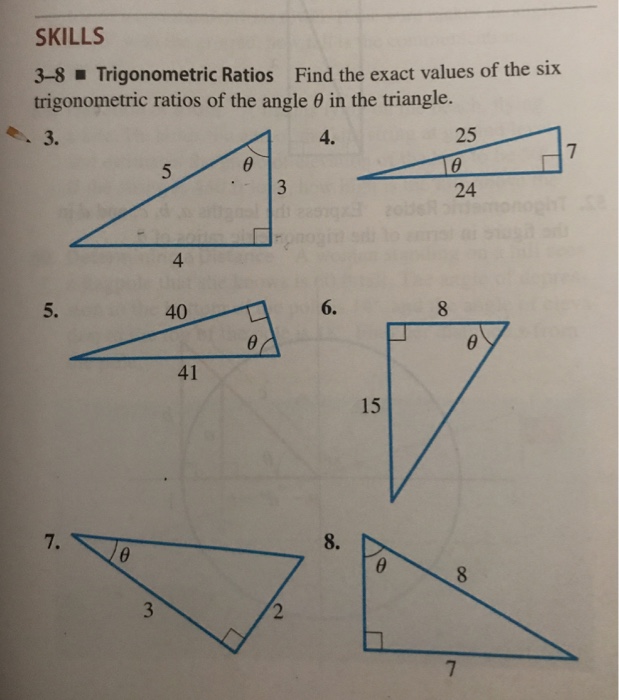



Solved Skills 3 S Trigonometric Ratios Find The Exact Values Chegg Com



How To Find The Values Of The Six Trigonometric Functions Given The Point 3 5 4 5 Which Lies On The Terminating Side Quora



Exact Trig Values




Intro To The Trigonometric Ratios Video Khan Academy




Special Right Triangle Wikipedia



1




Trigonometric Functions




Trigonometric Functions And Right Triangles Mathbootcamps




3 3 Points Find All Trigonometric Functions Of The Chegg Com




Applying Trig Functions To Angles Of Rotation Ck 12 Foundation
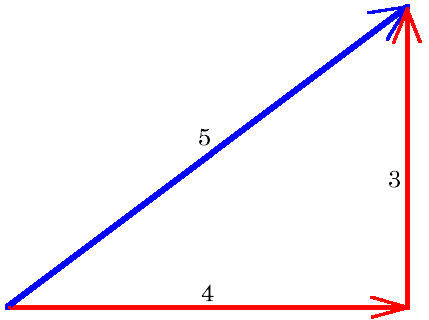



Getting Square With The 3 4 5 Triangle
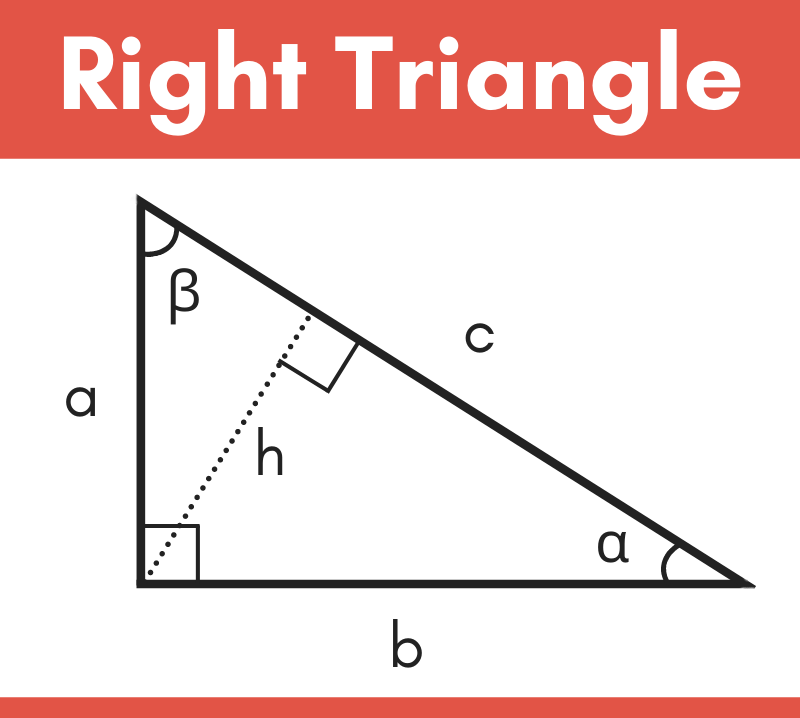



Right Triangle Calculator Solve Any Edge Or Angle Inch Calculator



What Is Sine Cosine And Tangent Socratic




Trigonometry




30 60 90 Triangle Explanation Examples




Math34 Trigonometric Formulas




3 4 5 Triangle Angles Radians




Right Triangle Trigonometry Review Article Khan Academy
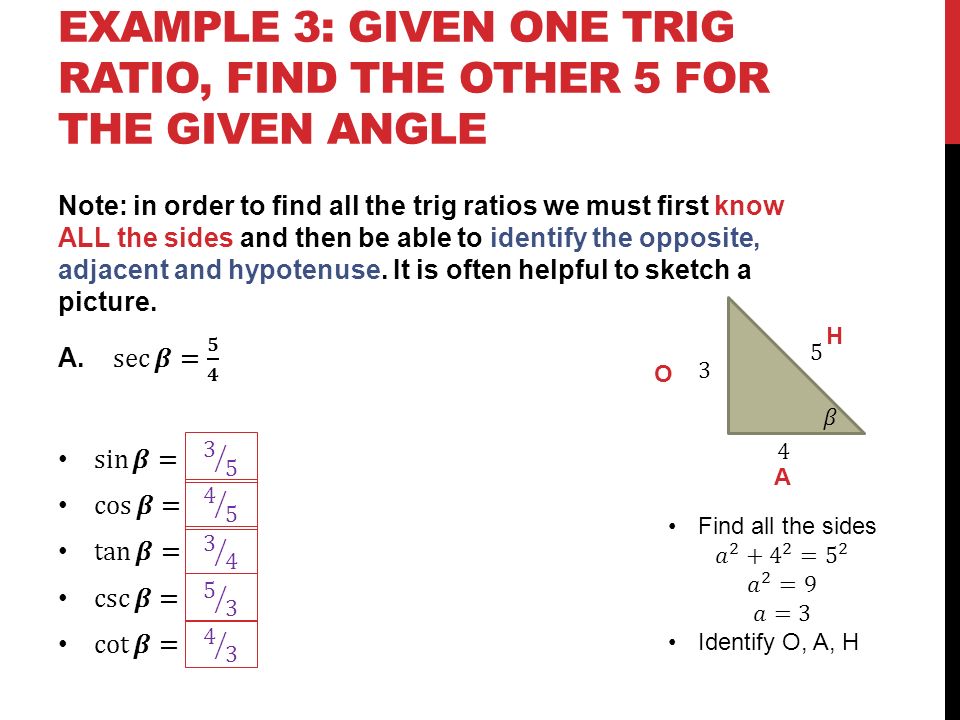



5 2 Trigonometric Ratios In Right Triangles Ppt Video Online Download




Manual Polygon Topo Builder




If Cos A 5 13 How Do You Find Sina And Tana Socratic



1



How To Solve Trigonometric Problems Complete Concrete Concise




Trigonometric Functions And Right Triangles Mathbootcamps
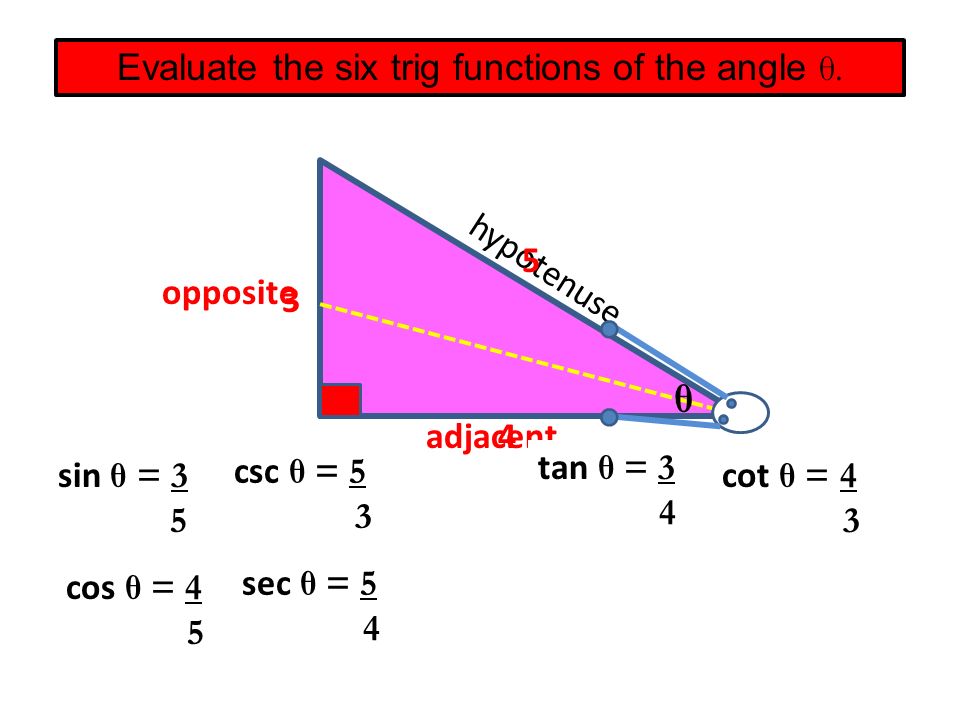



Trigonometry Right Triangles Non Right Triangles 1 Trig Functions Sin Cos Tan Csc Sec Cot 2 A 2 B 2 C 2 3 Radian Measure Of Angles 4 Unit Ppt Download




Trig Functions With A 3 4 5 Triangle Youtube




Example 1 Given Tan A 4 3 Find Other Ratios Chapter 8 Class 10




3 4 5 Triangle Angles Sides How To Solve Full Lesson
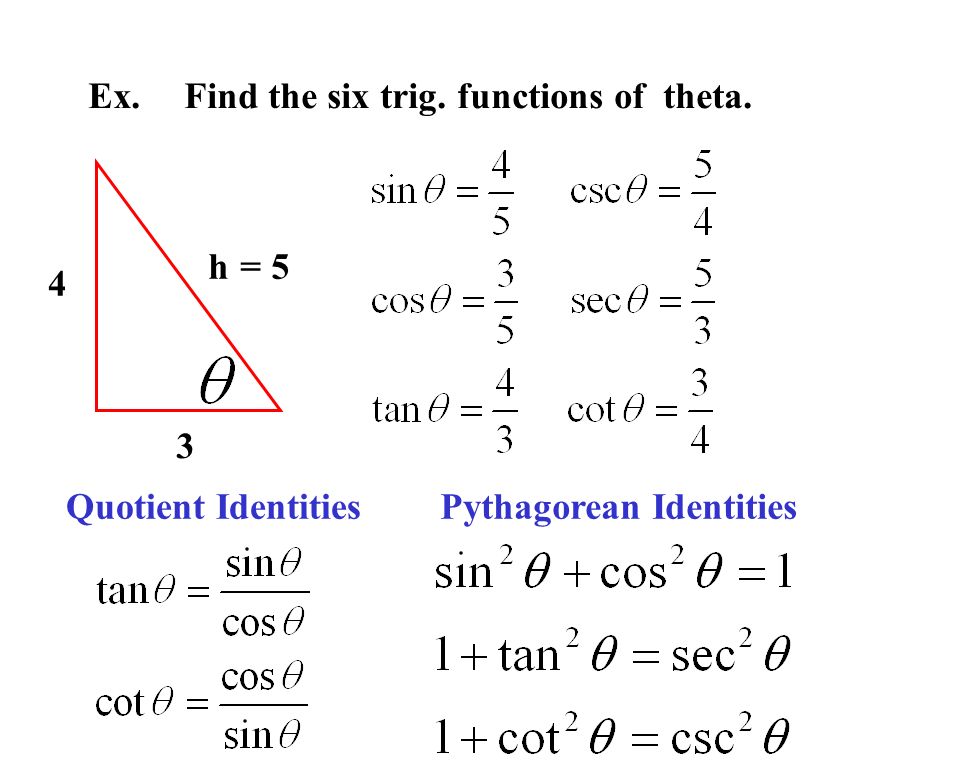



It S For Trigonometric Functions And Right Triangles 4 3 Right Triangle Trigonometry Adjacent Side Opposite Side Hypotenuse Ppt Download




Properties Of 3 4 5 Triangles Definition And Uses Video Lesson Transcript Study Com




Trigonometric Functions Of Any Angle Unit Circle Radians Degrees Coterminal Reference Angles Youtube



2



What Are The Angle Measurements Of A 3 4 5 Right Triangle Quora




Chapter 5 Trigonometric Functions Of Angles Opentextbookstore




Trig Unit Circle Review Article Khan Academy



Trigonometric Functions Of An Acute Angle Opencurriculum
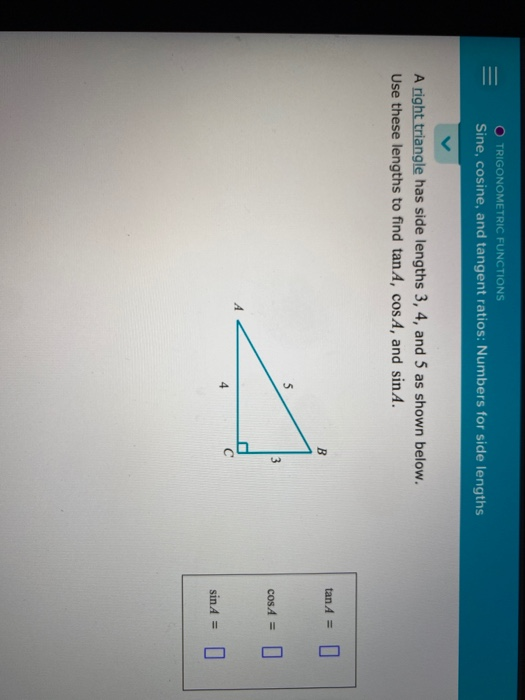



Trigonometric Functions Sine Cosine And Tangent Chegg Com




Download This Document Toolbox Pro V2




Special Right Triangles Fully Explained W 19 Examples



Lecture 2 Implicit Differentiation Inverse Trigonometric Functions Higher


